
Don’t believe the model, don’t ignore the model
De wet van behoud van ellende
Een goede raad: don’t believe the model: de werkelijkheid is altijd anders, rijker, gedetailleerder, genuanceerder en veelkleuriger. Nog een goede raad: don’t ignore the model, want goede modellen doen uitspraken over een stukje van de werkelijkheid, uitspraken die in veel gevallen waar zijn.
Vooral de combinatie van deze adviezen is waardevol: zonder het eerste advies is de verleiding groot het tweede in te korten tot: ‘modellen doen uitspraken over de werkelijkheid die waar zijn’. Samen geven ze het evenwicht dat het mogelijk maakt beschikbare modellen te onderzoeken en ze zinvol toe te passen als de situatie zich daarvoor leent.
Zoals de IT haar eigen modellen kent zo kennen ook andere disciplines hun eigen modellen. Dat zijn modellen die uitspraken doen die we niet zonder meer mogen vertalen naar ons vakgebied. Als we echter rekening houden met het ‘don't believe’, dan kunnen we er op een verantwoorde manier van profiteren.
In de komende maanden laat ik een aantal modellen uit andere disciplines de revue passeren. Dit keer is ‘de wet van behoud van ellende’ aan de beurt.
De wiskundige modellen van de natuurkunde sluiten zó goed aan bij onze waarneming dat we ze vaak niet als zodanig herkennen. We verwarren ze met de werkelijkheid. Don't believe the model, don't ignore the model kun je in dit verband zien als de parafrase van een uitspraak van Einstein: ‘Insofar as the laws of mathematics refer to reality, they are not certain; and insofar as they are certain, they do not refer to reality’.
De natuurkunde kent behoudswetten, wetten waarin wordt geformuleerd dat de totale waarde van een grootheid in een gesloten systeem niet verandert. De oudste en bekendste behoudswet is de wet van behoud van energie. De in praktijk gebrachte informatiekunde kent een variant daarop, de wet van behoud van ellende: elke oplossing voor een probleem introduceert haar eigen, nieuwe problemen. En zoals in een gesloten systeem de totale hoeveelheid energie niet verandert, zo blijft ook het totaal aan problemen gelijk. Eigenlijk is ‘behoud van ellende’ te negatief1: er is slechts sprake van behoud van problemen, wat impliceert dat eraan gewerkt moet worden, dat er (weer, meer) energie in moet worden gestoken. Waarschijnlijk is de desillusie — het gevolg van de confrontatie met onverwachte nieuwe problemen die de gevonden oplossing met zich meebrengt — debet aan de negatieve naam.
Behoud van ellende bestaat
Ter illustratie een greep uit het mei-nummer van informatie. Uit Succes is een keuze: ‘Telkens worden nieuwe tools op de markt gebracht als ‘oplossing’ en telkens worden slechts nieuwe problemen veroorzaakt.’ Uit En we noemen ’m...: ‘Leveranciers streven naar gebruikersgemak en dan is transparantie een vereiste. Transparantie kent echter haar prijs (...)’. Uit Wordt innovatie belemmerd door ITIL?: ‘Daarvoor is ITIL zeer geschikt. (...) Zolang dat (het oplossen van de door ITIL geïntroduceerde problemen, WL) niet gebeurt, is ITIL op termijn een gevaar voor het innovatief vermogen van de ICT-organisatie.’
Verklaringen
Voor bepaalde situaties verklaart de klok van Weick (zie het aprilnummer van informatie,) de wet van behoud van ellende: als een systeem niet tegelijkertijd algemeen, accuraat en eenvoudig kan zijn, dan betekent het kiezen voor het één het inleveren van iets anders.

Figuur 1: Simpele structuur, veel relaties
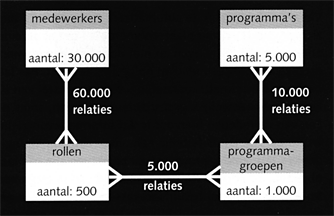
Figuur 2: Complexe structuur, weinig relaties
Naar analogie van energie kunnen we ook verschillende vormen van ellende onderscheiden. Neem bijvoorbeeld de autorisatieproblematiek —'mag medewerker x programma y uitvoeren?'— van een grote organisatie. In de oplossing van figuur 1 is de ellende het tijdrovende maar ongecompliceerde onderhouden van de vele relaties, de autorisaties. De oplossing daarvoor: structureer medewerkers in rollen, structureer programma's in samenhangende groepen en autoriseer vervolgens rollen voor programmagroepen. Dit reduceert het aantal relaties met meer dan 90 procent, maar introduceert nieuwe problemen, zoals het definiëren en beheren van rollen, en het toewijzen van medewerkers aan rollen. De ellende van het vele ongecompliceerde werk in combinatie met een simpele structuur, is omgezet in de structuur van figuur 2: veel minder ongecompliceerd werk maar een complexere structuur — met alle consequenties van dien.
Er is geen objectieve manier om ellende te kwantificeren. Daarom kunnen we op de wet van behoud van ellende niet zonder meer het etiket ‘waar’ plakken. De voorbeelden tonen echter aan dat behoud van ellende wel degelijk bestaat. Daarom is het verstandig er bij het ‘oplossen’ rekening mee te houden. Dat kan de desillusie waar deze wet haar naam aan te denken heeft, voorkómen.
Noot
1. Het Engels kent de wat beschaafdere uitdrukking ‘there is no free lunch’ als equivalent voor onze tactloos naamgegeven ‘wet van behoud van ellende’ In de vorm van ‘no free lunch‘-stellingen kent ook de informatica haar eigen, formele benadering van deze wet. De bekendste publicatie is No Free Lunch Theorems for Search van David H. Wolpert en William G. Macready (1996). Deze publicatie is als nfl.ps beschikbaar via ftp://ftp.santafe.edu/pub/wgm/
Zie voor meer informatie ook http://lucy.ipk.fhg.de/~mario/nfl/nfl.html.
[Beide hiervoor genoemde links leiden inmiddels tot niets. Een goed alternatief beginpunt is http://www.no-free-lunch.org. WL, 15 maart 2009]

