
Don’t believe the model, don’t ignore the model
Fuzzy logic—only available in Dutch
Een goede raad: don’t believe the model: de werkelijkheid is altijd anders, rijker, gedetailleerder, genuanceerder en veelkleuriger. Nog een goede raad: don’t ignore the model, want goede modellen doen uitspraken over een stukje van de werkelijkheid, uitspraken die in veel gevallen waar zijn.
Vooral de combinatie van deze adviezen is waardevol: zonder het eerste advies is de verleiding groot het tweede in te korten tot: ‘modellen doen uitspraken over de werkelijkheid die waar zijn’. Samen geven ze het evenwicht dat het mogelijk maakt beschikbare modellen te onderzoeken en ze zinvol toe te passen als de situatie zich daarvoor leent.
Zoals de IT haar eigen modellen kent zo kennen ook andere disciplines hun eigen modellen. Dat zijn modellen die uitspraken doen die we niet zonder meer mogen vertalen naar ons vakgebied. Als we echter rekening houden met het ‘don’t believe’, dan kunnen we er op een verantwoorde manier van profiteren. Deze maand wordt de term vage logica onder de loep genomen.
Vage logica, dat klinkt als een contradictie, en dat zou het ook zijn als de logica vaag zou zijn. Vage logica (fuzzy logic) is niet zelf vaag, maar biedt de ruimte om uitspraken te doen over begrippen, onderwerpen en situaties die een zekere mate van vaagheid kennen — en is niet alles tot op zekere hoogte vaag?
De termen van de taal
Steeds sta je als schrijver voor de keuze tussen Engelstalige en Nederlandstalige begrippen. Fuzzy logic klinkt velen waarschijnlijk bekender in de oren dan vage logica, en dat zal ook wel gelden voor fuzzy sets (vage verzamelingen) en truth values (waarheidswaarden). De informatie over vage logica op de site van de Hogeschool van Amsterdam deed me besluiten de Nederlandse termen te gebruiken. Tegelijkertijd realiseerde ik me dat kiezen voor het Engelstalige of het Nederlandstalige begrip een voorbeeld is van een vaag proces. Check it out!
Bart Kosko (Kosko, 1993) confronteert de lezer aan het begin van het eerste hoofdstuk van zijn boek Fuzzy Thinking direct met het vage denken: ‘Neem een appel in je hand. Is het een appel? Ja. Het ding in je hand hoort bij de stukjes ruimte-tijd die we de verzameling appels noemen — alle appels altijd overal. Neem nu een hap, kauw hem en slik hem door. Laat je spijsverteringskanaal de moleculen van de appel ontleden. Is het ding in je hand nog steeds een appel? Ja of nee? Neem nog een hap. Is het nog steeds een appel? Neem nog een hap, en zo verder tot er niets meer over is. De appel verandert van ding in niet-ding, in niets. Maar waar passeert hij de lijn tussen appel en niet-appel?…
Wiskunde naar smaak toevoegen
Veel verhandelingen over vage logica duiken al snel in ‘de wiskunde’ om daar vervolgens niet meer uit te komen. Ik wil geen afbreuk doen aan het (maatschappelijke) belang daarvan: fuzzy controllers zitten tenslotte in onze wasmachines, in onze foto-en videocamera’s, in onze centrale verwarmingssystemen, in de F16’s van onze KLu en in de 747’s van onze KLM. En helemaal zonder wiskunde lukt het overigens ook niet, omdat vage verzamelingen de basis van de vage logica zijn. Daarom een snufje wiskunde. Daar kun je zelf zo veel aan toevoegen als je wilt: de vraag ‘What is fuzzy logic’ aan AltaVista resulteerde in 135 pages found.1 De klassieke verzamelingenleer kent het begrip deelverzameling. Van elk element in een verzameling kan worden aangegeven of het al dan niet tot een bepaalde deelverzameling behoort. Neem bijvoorbeeld de verzameling P van alle personen die in Nederland wonen. De verzameling M van alle mannen die in Nederland wonen is een deelverzameling van P. De verzameling M kan worden geconstrueerd door voor elk element p van P te bepalen of de uitspraak ‘p is een man’ waar is. Het resultaat hiervan is een verzameling geordende paren waarin bijvoorbeeld voorkomen: {Rick van der Ploeg; 1}; {Vera Keur; 0}; {Conny Palmen; 0} en {Gerrit Komrij; 1} (waarbij I staat voor ‘waar’ en 0 voor ‘onwaar’). Vaststellen of een element p van P tot M behoort, is nu eenvoudig: zoek de persoon op in de verzameling geordende paren, en de bijbehorende waarheidswaarde geeft aan of het element tot de deelverzameling M behoort. Kenmerk van de klassieke verzameling is dat een element ertoe behoort of er niet toe behoort, andere mogelijkheden zijn er niet.
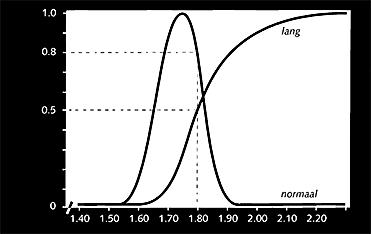
Figuur 1
Vage (deel)verzamelingen kunnen we op een vergelijkbare manier construeren. Het verschil is dat als waarheidswaarden nu alle waarden vanaf 0 tot en met 1 kunnen voorkomen. Het meest gebruikte voorbeeld voor een vage verzameling is de verzameling lange mannen. Een man van 1,80 meter lang heeft dan bijvoorbeeld een waarheidswaarde van 0,5 (ook wel lidmaatschapsfunctiewaarde genoemd). Dezelfde man kan ook lid zijn van de verzameling mannen met normale lengte, bijvoorbeeld met een lidmaatschapsfunctiewaarde van 0,8 (zie figuur 1). Het verschil met conventionele verzamelingen is dat er sprake kan zijn van wat je een ‘deellidmaatschap’ kunt noemen. Behalve dat een element er niet (0) of helemaal (1) toe kan behoren, kan het er als het ware voor een deel toe behoren.
Vage verzamelingen versus kansrekening
Het woord ‘vaag’ roept bij velen een negatief gevoel op. De oplossing lijkt om de vaagheid te ontkennen en te vertalen in begrippen als onzekerheid, risico en toeval. Want daarvan weten we ten minste hoe we ermee moeten omgaan… Dat helpt echter niet: de meeste vaagheid gaat gepaard met een grote precisie. Van de appel waarvan je al vier happen genomen hebt kun je precies vaststellen hoeveel procent van het oorspronkelijke gewicht nog over is. Maar die precisie helpt niet bij het vaststellen van de grens tussen appel en niet-appel.
Vage verzamelingen en waarschijnlijkheidstheorie liggen dicht bij elkaar, maar zijn niet hetzelfde. Kansrekening zegt iets over de kans op kop of munt, maar het resultaat is óf kop, óf munt, niet iets daartussenin met kenmerken van beide. Een mooi voorbeeld van het verschil tussen een vage verzameling en een kans staat op de site van de Hogeschool van Amsterdam2: uit welke fles drink je als je dreigt om te komen van de dorst: uit de fles waarvan je weet dat de kans dat de inhoud drinkbaar is 90 procent bedraagt, of uit de fles waarvan de inhoud een lidmaatschapsfunctiewaarde van 0,9 van de verzameling ‘drinkbare vloeistoffen’ heeft?

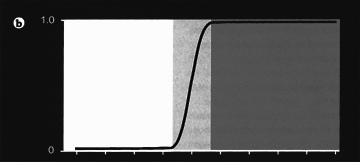
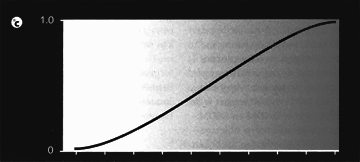
Figuur 2a tm c
Ontkennen helpt niet!
Het 0-1-denken dat ons informatici zo gewoon is, verleidt ons te streven naar overgangen zoals die van figuur 2a. Duidelijke overgangen, dat wil zeggen: een zo klein mogelijk grijs gebied tussen wit en zwart. Als de breedte van het ‘grijze’ gebied heel klein is, zoals in figuur 2b, kunnen we zonder al te veel problemen doen alsof er helemaal geen grijs gebied is. We hoeven dan alleen te voorzien in de situaties ‘wit’ en ‘zwart’. In werkelijkheid is het grijze gebied meestal groter dan we leuk vinden, met als gevolg dat we rekening moeten houden met een heel scala aan ‘grijstinten’, zoals weergegeven in figuur 2c.
Over mannen en vrouwen…
Personen indelen in mannen en vrouwen lijkt op het eerste gezicht een simpel voorbeeld van tweewaardige logica. Er zijn maar twee geslachten: mannen en vrouwen. Dus: ‘Als hij geen man is, is zij een vrouw’. De werkelijkheid is ingewikkelder: als we als criterium voor ‘is man’ de uitwendige geslachtsorganen nemen, krijgen we een andere deelverzameling ‘mannen’ dan wanneer we als criterium het hebben van slechts één X-chromosoom gebruiken. Een leesbaar boek over dit op zich boeiende onderwerp is Eve’s Rib (Pool, 1994). De moeite die het kost om de criteria voor ‘is man’ te beschrijven, ondersteunen de suggestie dat alle begrippen (buiten de wiskunde?) tot op zekere hoogte vaag zijn.
Veel vaagheid zit in variaties op het thema ‘continue variabelen die we in discrete vakjes willen stoppen’: zij is lang, het is warm, een moerassige bodem, een lange verwerkingstijd, veel mutaties. Een andere categorie waarmee we in ons werk te maken hebben zijn de vaagheden die het gevolg zijn van geleidelijke verandering in de tijd. We praten over onze projecten alsof de fasen gescheiden zijn zoals in figuur 2a. Een voorbeeld: eerst zetten we de architectuur op, daarna ontwikkelen we onze systemen conform de geformuleerde architectuur. In werkelijkheid is er geen duidelijke lijn te trekken tussen architectureren en ontwerpen (net zo min als tussen lang en kort of tussen warm en heet). De figuren 2b en 2c geven een realistischer beeld. Een beeld dat ons duidelijk maakt dat we beter kunnen leren omgaan met vage situaties dan onze energie te stoppen in het ontkennen ervan.
Literatuur
Kosko, Bart: Fuzzy Thinking, The New Science of Fuzzy Logic, Hyperion Books, 1994.
Pool, Robert: Eve’s Rib, Crown, 1994. Nederlandse vertaling: Eva’s rib, Forum.
Noten
1. Aanbevolen: http://www.cs.cmu.edu/Web/Groups/AI/html/faqs/ai/fuzzy/part1/faq.html en de in noot 2 genoemde site van de Hogeschool van Amsterdam.
2. http://htsa.htsa.hva.nl/~pylgroms/fuzzylog.htm [404, WL, 15-3-2010].

