
Don’t believe the model, don’t ignore the model
Chaos as destiny—only available in Dutch
Een goede raad: don’t believe the model: de werkelijkheid is altijd anders, rijker, gedetailleerder, genuanceerder en veelkleuriger. Nog een goede raad: don’t ignore the model, want goede modellen doen uitspraken over een stukje van de werkelijkheid, uitspraken die in veel gevallen waar zijn.
Vooral de combinatie van deze adviezen is waardevol: zonder het eerste advies is de verleiding groot het tweede in te korten tot: ‘modellen doen uitspraken over de werkelijkheid die waar zijn’. Samen geven ze het evenwicht dat het mogelijk maakt beschikbare modellen te onderzoeken en ze zinvol toe te passen als de situatie zich daarvoor leent.
Zoals de IT haar eigen modellen kent zo kennen ook andere disciplines hun eigen modellen. Dat zijn modellen die uitspraken doen die we niet zonder meer mogen vertalen naar ons vakgebied. Als we echter rekening houden met het ‘don’t believe’, dan kunnen we er op een verantwoorde manier van profiteren.
In dit licht wil ik deze keer ‘de wet van toenemende entropie’ bespreken.
Dit voorjaar was ik op Mallorca. Stukken land zijn daar van elkaar gescheiden door lage muren. Er zijn muren die net nieuw zijn, maar je ziet er ook die nog maar nauwelijks als muur herkenbaar zijn. En alles daartussenin. Een enkele keer zie je ook mensen nieuwe muren bouwen of bestaande muren herstellen.
Toenemende entropie
Vorige maand was het onderwerp ‘de wet van behoud van ellende’, naar analogie van de Eerste Wet van de thermodynamica, de wet van behoud van energie. Deze maand staat de Tweede Wet centraal. De bekendste formulering van de Tweede Wet is de wet van toenemende entropie, de mate waarin orde afwezig is: spontaan verlopende processen leiden (in een gesloten systeem) altijd tot een toename van entropie, nooit tot een afname.
‘Behoud van ellende’ kan nog positief uitgelegd worden: het blijft gelijk, het neemt dus niet toe. De wetmatigheid van toenemende entropie echter betekent een onomkeerbaar proces richting chaos.
Entropie, orde en chaos
Entropie, orde en chaos zijn lastige begrippen. Het volgende voorbeeld, ontleend aan Devaney (1990), is bedoeld om aan te geven dat voorzichtigheid bij het gebruik van deze begrippen geboden is.
De logistieke functie f(x) =cx(1 - x) speelt een belangrijke rol bij het berekenen van de omvang van een populatie in de loop van de tijd. Het itereren van deze functie met behulp van het voorschrift xt+1 =cxt - cxt2 leidt tot geheel verschillende patronen voor verschillende waarden van c en x0. Zie voor een voorbeeld tabel 1.
De vraag die hier gesteld kan worden is: ‘is hier nu sprake van ‘orde’ omdat we een ordelijk model hebben in de vorm van een simpele functie en een simpel iteratieproces, of is dit ‘chaos’ omdat we te maken hebben met een verloop van uitvoerwaarden dat chaotisch kan zijn?’ Als we die vraag niet kunnen beantwoorden, kunnen we vanzelfsprekend ook niets zeggen over de entropie in zo’n systeem.
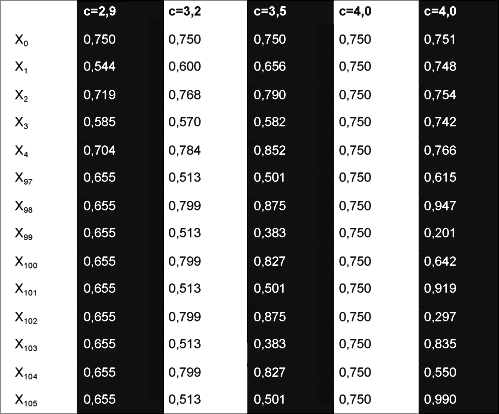
Tabel 1: Resulterende xn voor verschillende waarden van c en x0
Is chaos onvermijdelijk?
De Tweede Wet heeft betrekking op thermodynamische verschijnselen. In het laatste hoofdstuk van Chaos (Gleick, 1988)1 lezen we er het volgende over:
‘Everything tends toward disorder. (...) However expressed, the Second Law is a rule from which there seems no appeal. In thermodynamics that is true. But the Second Law has had a life on its own in intellectual realms far removed from science. (...) These secondary, metaphorical incarnations of the Second Law now seem especially misguided. In our world, complexity flourishes, and those looking to science for a general understanding of nature’s habits will be better served by the laws of chaos.’
Dit is een duidelijke ‘don’t believe’-suggestie: wees voorzichtig met analogieën en zoek vooral ook elders. De wet van toenemende entropie mag blijkbaar niet zonder meer worden toegepast op andere terreinen. Maar met die waarschuwing in gedachten valt er van de analogie wel wat te leren. De analogie impliceert niet dat systemen in de loop van de tijd chaotischer worden, maar wel dat er energie nodig is om dit te voorkomen. Energie die er bij de muren op Mallorca wordt ingestopt door de mensen die zich bezighouden met het onderhoud. Het onderhoud dat, over de jaren heen, veel meer tijd kost dan het oorspronkelijke bouwen of graven. Het onderhoud dat, als het goed wordt uitgevoerd, voor de incidentele toeschouwer de suggestie wekt dat de muren en sloten ‘als nieuw’ zijn en blijven zonder noemenswaardige inspanning.
Hoe komt het toch dat wij, IT’ers, zo goed begrijpen dat muren onderhoud vergen, maar dat we in ons eigen werk kwaliteitssystemen opzetten zonder audits te laten uitvoeren? Dat we grote, complexe systemen aanbieden aan gebruikersorganisaties zonder te voorzien in goed onderhoud? Komt het omdat we denken dat onze systemen uit nullen en enen bestaan die niet vatbaar zijn voor verval? Vergeten we dat onze systemen deel zijn van een groter geheel? Een groter geheel waarin personeelswisselingen, nieuwe producten, wijzigingen in de afspraken met afnemers en wijzigingen in de organisatie hun invloed hebben. En zoals de planten hun wortels steeds dieper de muren op Mallorca in laten groeien om ze, geholpen door regen en wind, langzaam maar zeker af te breken, zo vergaat het ook onze systemen. Maar gelukkig zijn onze systemen open systemen. Daarom is er een remedie tegen de chaos die ze bedreigt: er voldoende energie in steken.
Noot
1 Voor diegenen die onbekend zijn met het gebied van dynamische systemen is behalve het boek van Gleick ook Complexity (Waldrop, 1992) een leesbare introductie. Een goed startpunt op Internet is www.santafe.edu.
Literatuur
Devaney, Robert L.: Chaos, Fractals and Dynamics: Computer Experiments in Mathematics, Addison-Wesley, 1990.
Gleick, James: Chaos: Making a New Science, Penguin, 1988.
Waldrop, M. Mitchell: Complexity: The Emerging Science at the Edge of Order and Chaos, Simon & Schuster, 1992.

